データサイエンス、機械学習、ブロックチェーンなど、数学理論に裏打ちされた技術に注目が集まっています。それに従い、エンジニアにも数学の知識がより必要になってきているのは、良く耳にするところ。そこで、高校数学を学び直せるクイズを用意!さあ、あなたは何問解ける!?

問題5. 確率が分かると円周率が計算できる!?【Pythonで学び直す高校数学】
機械学習に注目が集まっていることは、ご存知の方も多いでしょう。機械学習とは、大量のデータを使って反復的に学習することによって、何らかの特徴を見つけ出す技術です。インターネットのショッピングサイトで表示される「あなたにおすすめの商品」や、看板などに書かれた文字をカメラで撮影するだけで翻訳してくれるアプリなど、機械学習の技術は私たちの身近なところですでにたくさん使われています。機械学習の分野で活躍したいなら、確率についてしっかり学んでおきましょう。
「サイコロを振る」が試行、「1の目が出る」が事象
サイコロを振ったときに「1」の目が出る確率は1/6、明日の降水確率は20%、宝くじで1等が当たる確率は……。このように確率という言葉は日常生活でよく使います。数学の世界では「ある試行を行ったとき、その結果として起こりうるすべての事象のうち、特定の事象になる割合」を確率と言います。
試行とは「サイコロを振る」「コインを投げ上げる」のように、同じ条件で何度も繰り返すことができて、その結果が偶然に左右されるもので、事象とは「1の目が出る」や「表が出る」など、試行の結果として起こる出来事です。
サイコロを振ったときに1の目が出ることを事象Aとすると、事象Aが起こる確率pは、

確率pを求める式
で求めることができます。確率を表す記号には「p/i>」がよく利用されますが、これはprobability(確率)の頭文字です。
この式で計算すると、サイコロを振ったときに1の目が出る確率は1/6ですが、これは「何度も試行を繰り返していくと、最終的に1の目が出る確率はおよそ1/6になる」という意味です。6回サイコロを振ったら必ず1が出るということではないので注意してください。
また、確率pの範囲は必ず、
0≦p≦1
になります。もしp=0ならば、その事象が起こる可能性がないことを表しています。逆にp=1ならば、その事象は必ず起こるということです。
さて、サイコロを何回も振ったら、最終的に1の目が出る確率は1/6になる――。本当かどうか、確かめてみましょう。
※本連載ではPythonを実行する環境として、Anacondaディストリビューションのインストールを前提にしています。簡単な使い方は第1回「10進数と2進数――その違い、わかりますか?」と第2回「方程式をもとにPythonでグラフを描いてみましょう」で解説していますが、くわしく解説しているサイトもたくさんあります。PythonやAnacondaを操作したことがないという人は、そうしたサイトもぜひ参考にしてみてください。
【問題】1の目が出る確率が1/6になることを確かめてください
実際にサイコロを振って確かめてみてもいいのですが、「同じことの繰り返し」にはプログラムを使うのが有効です。そこでPythonでサイコロを振るプログラムを作ってみました。
1:import random 2: 3:# サイコロを振る 4:cnt = 0 # 1が出た回数を記録する変数を定義(初期値は0) 5: 6:for i in range(10000): 7: dice = random.randint(1, 6) 8: if dice == 1: 9: cnt += 1 10: 11:# 確率を求める 12:p = cnt / 10000 13:print(p)
このプログラムでは、4~9行目のforループにより、以下の処理を10000回繰り返すようにしています。
まず、サイコロを振る代わりに
dice = random.randint(1, 6)
を実行することで、1~6までの整数のうち、どれか1つをランダムに選びます。ちなみに、ランダムに選ばれた数が乱数です。
この値が1のときに変数cntに1を加えるようにします。これにより、1が出た回数を数えることができます。
ループを終了したあとの12行目で
p = cnt / 10000
を計算することにより、1が出た回数を試行回数で割って確率を求めています。
※環境によっては、整数同士の計算結果が整数になる場合があります。pが0になってしまう場合は、12行目の「10000」を「10000.0」に書き換えてください。
なお、結果は実行するたびに変わります。それは、randint()関数が選ぶ値が毎回変わるからです。実際にサイコロを振ったときに出る目が常に同じパターンではないのと同じですね。
【問題】確率を使って円周率を算出する方法を考えてみましょう
次に「モンテカルロ法」と呼ばれる、ちょっとおもしろい計算を紹介しましょう。これは、確率を使って、確率とはまったく関係ない問題を解く手法です。例題として最もポピュラーなのは、円周率を求める問題です。そう、確率を使うと円周率を求めることができるのです。
それだけではどうすればいいのか、すぐには思い浮かばないかもしれません。図を見ながら、一歩ずつ考えていきましょう。
以下の図は、半径が50の円と、それに外接する正方形です。円の半径が50なので、正方形の1辺は50×2、すなわち100ですね。
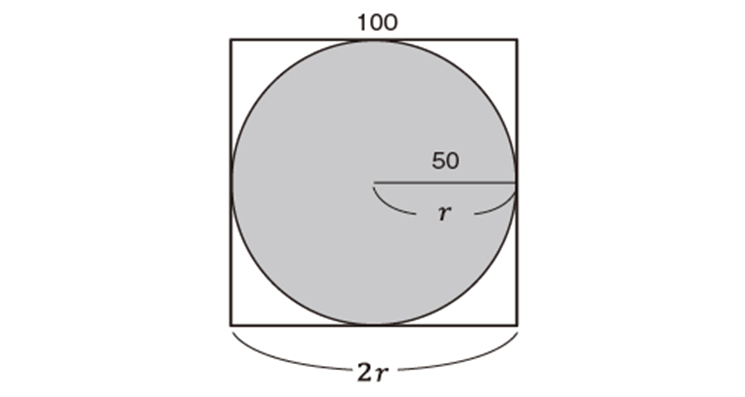
円とそれに外接する四角形
この中にランダムに点を打っていくとしましょう。円の面積はπr2で、この円に外接する正方形の面積は4πr2(=2r×2r)です。この四角形の中のランダムな位置に点を打つとき、
その点が円の中に入る確率pは、
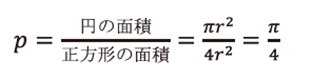
ランダムに打った点が円の中に入る確率
となります。さらにこの式を変形すると、π=4pとなります。どうでしょう。ランダムに打った点が円内に入る確率を計算すれば、円周率を計算できますね。
先に、この考えに従って作ったプログラムを見てもらいましょう。
1:%matplotlib inline
2:import matplotlib.pyplot as plt
3:import random
4:import math
5:
6:cnt = 0
7:for i in range(3000):
8: x = random.randint(1, 100)
9: y = random.randint(1, 100)
10: d = math.sqrt((x-50)**2 + (y-50)**2 )
11: if(d <= 50 ):
12: cnt += 1
13: plt.scatter(x, y, marker=".", c="r")
14: else:
15: plt.scatter(x, y, marker=".", c="g")
16:plt.axis('equal')
17:plt.show()
18:
19:p = cnt / 3000
20:pi = p * 4
21:print(pi)
7行目からのforループで、正方形の中に打つ点をランダムに生成し、それが円の中に収まっているかどうかを判断しています。
具体的には、8行目と9行目でぞれぞれ、x座標とy座標をランダムに決めています。値は1~100の整数です。
ここでは(50, 50)を中心と考えます。この中心と生成した点との距離を割り出します。計算をしているのが10行目で、変数dがこの距離に当たります。
距離を割り出すには、三平方の定理、またの名をピタゴラスの定理を使います。覚えていますか? この定理は、「直角三角形の斜辺の長さは、残りの2辺の長さを2乗して足したものと等しい」というものです。これを上記のプログラムに当てはめたのが以下の図です。
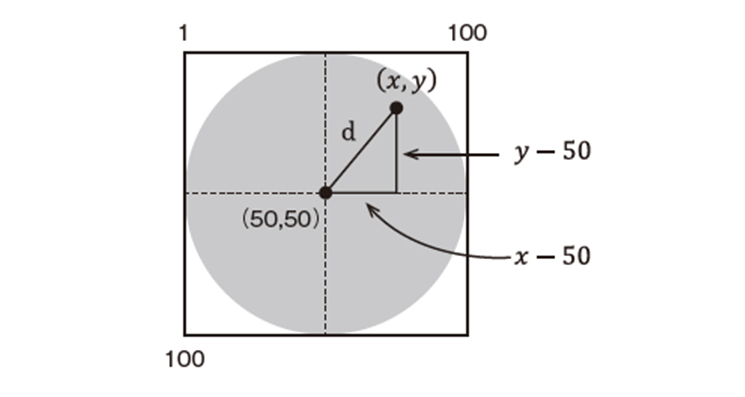
円の中心と生成した点の距離
生成した点と中心を結んだ線が、直角三角形の斜辺にあたります。のこりの2辺は中心からx座標までの距離(水平方向)と、中心からy座標までの距離(垂直方向)です。生成された点の座標はプログラムの中では変数xと変数y、中心の座標は(50, 50)です。ピタゴラスの定理に当てはめれば、「d2=(x-50)2+(y-50)2」になります。この式の左辺はd2ですから、両辺の平方根を取るとdの値が求められます。
この計算をしているのが、10行目の、
d = math.sqrt((x-50)**2 + (y-50)**2 )
です。「math.sqrt」でmathライブラリのsqrt()関数を呼び出しています。2乗はPythonでは「**2」と記述します。
ここで求めたdの値が50以下なら円の中かどうかを判断しているのが11行目です。この条件に当てはまる点は赤、当てはまらない点は緑で表示するようにすると同時に、当てはまる点の数をカウントします。その処理を、12~15行目で行っています。
最後に、円内の点の数を全体で割って(19行目)、その数値を4倍します(20行目)。さて、どうなるでしょう。このプログラムを実行した結果、
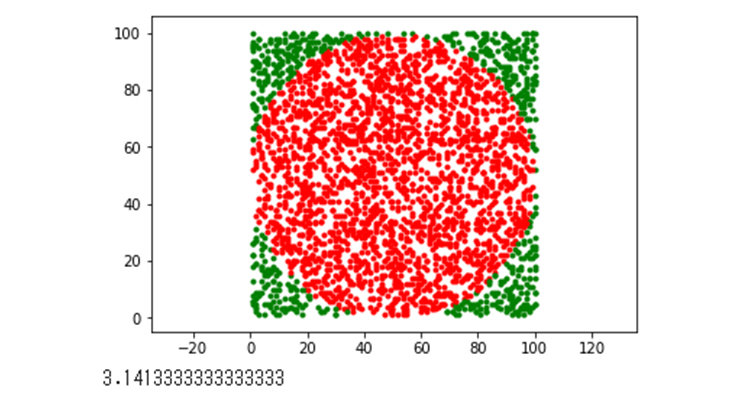
プログラムを実行した結果
かなり満足のいく数値が出てきました。乱数で点の位置を決めているので、プログラムを実行するたびに結果の数値は変わります。試行回数が多いほど、精度は上がります。ただし、結果が出るまでの処理時間も長くなります。13~17行目までをコメントアウトする(行頭に#を追加する)と、描画を省略できて全体が高速に処理できます。プログラム中の「3000」を書き換えて、ぜひ精度の高い計算も試してください。
文/仙石 誠(日経BP)

文系出身者でも分かりやすいと評判の数学【再】入門書。単に数学理論を解説するだけでなく、Pythonコードで確かめられるところが好評です。
著者:谷尻かおり(メディックエンジニアリング)
価格:2500円+税
RELATED関連記事
JOB BOARD編集部オススメ求人特集
RANKING人気記事ランキング

年収2500万でも貧困層? 米マイクロソフトに18年勤務した日本人エンジニアが「日本は健全」と語るワケ

AIを「便利な道具」と思う限り、日本に勝機はない。AI研究者・鹿子木宏明が語る“ズレたAIファースト”の正体

「アジャイルの理屈を押し付けない」大手金融機関が10年かけて実践した“アジャイル文化”作りの裏側

落合陽一「2026年にはほとんどの知的作業がAIに置き換わる」人間に残される仕事は“とげ作り”

AWS認定資格12種類を一覧で解説! 難易度や費用、おすすめの学習方法も
タグ

















