データサイエンス、機械学習、ブロックチェーンなど、数学理論に裏打ちされた技術に注目が集まっています。それに従い、エンジニアにも数学の知識がより必要になってきているのは、良く耳にするところ。そこで、高校数学を学び直せるクイズを用意!さあ、あなたは何問解ける!?

問題3.連立方程式を解くプログラムを作れますか?【Pythonで学び直す高校数学】
前回の「方程式を元にPythonでグラフを描けますか?」では、あらかじめ決められた2点を通る直線の方程式を求めました。その計算をPythonでプログラミングして、方程式が示す直線をグラフで表すところまで解説しました。
今回はもう少し方程式の解き方を掘り下げてみましょう。まずは、2本の直線をグラフ化するプログラムコードを見るために、ある直線と垂直に交わる直線を求めます。
本連載ではPythonを実行する環境として、Anacondaディストリビューションのインストールを前提にしています。簡単な使い方は第1回「10進数と2進数――その違い、わかりますか?」と第2回「方程式を元にPythonでグラフを描けますか?」で解説していますが、詳しく解説しているサイトもたくさんあります。PythonやAnacondaを操作したことがないという人は、そうしたサイトもぜひ参考にしてみてください
【問題】点(1, 5)を通ってy=1/2x+1/2と直交する直線を求めよ
「直交する」とは、垂直に交わるということです。2つの直線の方程式で見てみましょう。
y=a1x+b1とy=a2x+b2という2つの直線の方程式があるとき、a1とa2に注目します。
もしa1=a2であれば、2つの直線は平行になります。
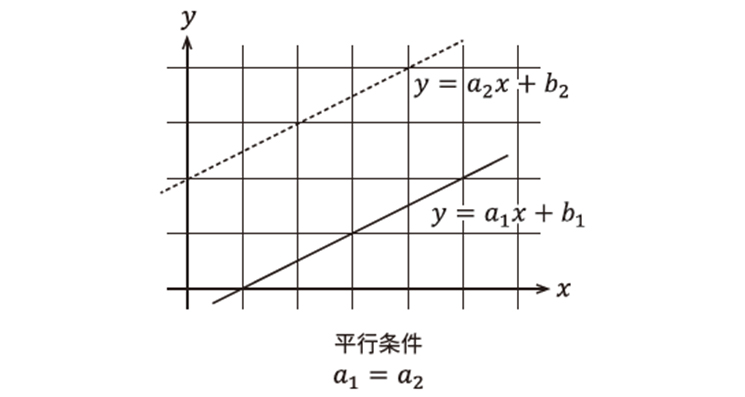
a1=a2ならば2本の直線は平行
もしa1×a2=-1のとき、2つの直線は垂直に交わります。
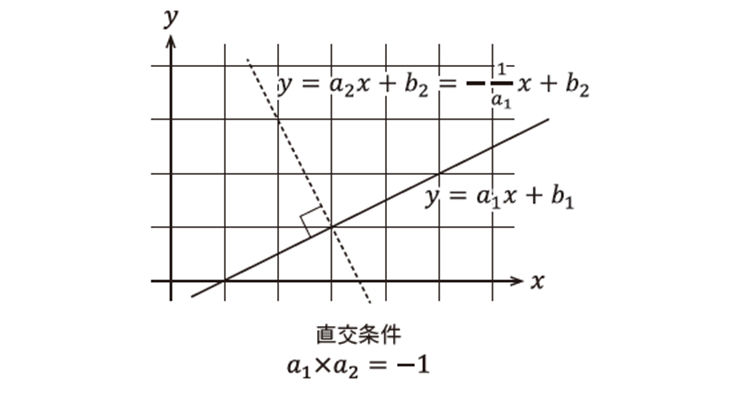
a1×a2=-1ならば2本の直線は直交
a1=a2が直線の平行条件、a1×a2=-1が直線の直交条件です。
では、点(1, 5)を通って、下の図の点線で示したy=1/2x+1/2と直交する直線を求めてみましょう。
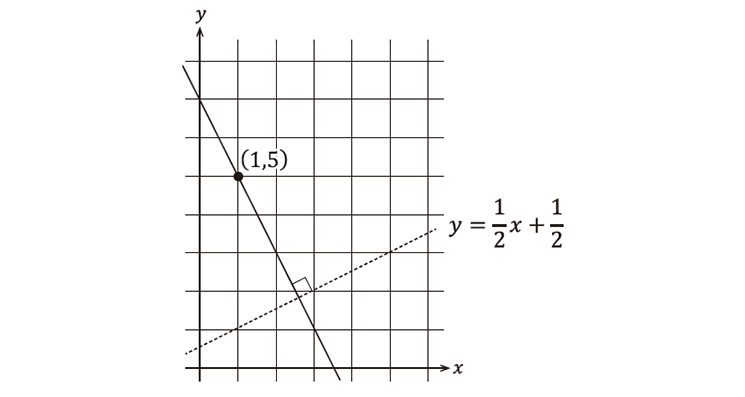
(1, 5)を通ってy=1/2x+1/2と直交する直線
直線の傾きaは直線の直交条件により、
1/2×a=-1
a=-2
求めた傾きaと指定された座標(1, 5)をy=ax+bに代入すると、
5=-2×1+b
b=7
つまり、求める直線の式はy=-2x+7とわかりました。では、Pythonのプログラムでこの計算結果が正しいかどうか、確かめてみましょう。
以下のリストは、今求めた直線がもとの直線と本当に直交するか、確認するプログラムです。
1: %matplotlib inline
2: import matplotlib.pyplot as plt
3: import numpy as np
4:
5: x = np.arange(-1, 6) # xの範囲を決めておく
6: y = 1/2 * x + 1/2 # 直線1の式
7: y2 = -2 * x + 7 # 直線1に直交する直線の式
8:
9: # グラフを描画
10: plt.plot(x, y)
11: plt.plt(x, y2)
12: plt.axis('equal')
13: plt.grid(color='0.8')
14: plt.show()
このプログラムではもとの直線をy、この直線に直交する直線をy2と定義しています(6~7行目)。matplotlibは特に何も指定しないとグラフ全体が描画されるように目盛りの大きさを自動調整してしまいます。今回は2本の直線が直交することを確認したいので、12行目でplt.axis('equal')を実行しています。これにより、x軸とy軸の目盛りの増分が等しくなります。このリストをJupyter Notebookで実行した結果が次の図です。
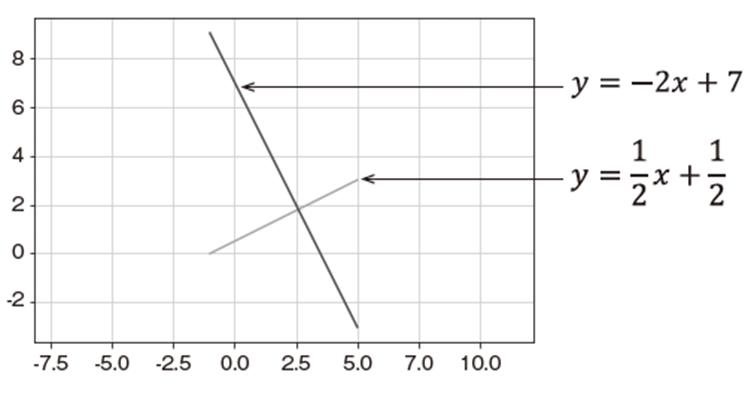
y=(1/2)x+(1/2)とy=-2x+7のグラフ
2本の直線が直交していることが見て取れますね。
【問題】2本の直線の交点はどうやって求めますか
もう一問、方程式を解いてみましょう。今度は、同一平面上に2本の直線があります。この2直線は平行でない限り、必ずどこか1点で交わります。その交点を求めてください。
この交点は、2つの直線の式を同時に満たす点です。つまり、連立方程式の解になります。グラフで示すと、下の図の(x, y)が求める交点になります。
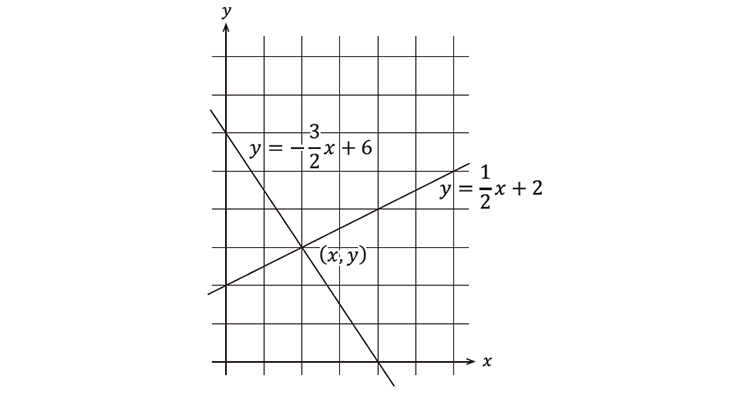
2直線の交点
この2本の直線の式はそれぞれ、
y=-3/2x+6
y=1/2x+2
です。連立方程式を解くには、PythonのライブラリであるSympyのsolve()関数を使います。Pythonインタプリタで以下のように実行してみると、交点の座標が(2, 3)であることがわかります。
※Pythonインタプリタの使い方は第2回「方程式をもとにPythonでグラフを描いてみましょう」を参照してください。
>>> from sympy import Symbol, solve
>>> x = Symbol('x')
>>> y = Symbol('y')
>>> ex1 = -3/2 * x + 6 - y
>>> ex2 = 1/2 *x + 2 - y
>>> print(solve((ex1, ex2)))
{x: 2.00000000000000, y: 3.00000000000000}
ここでは、2~3行目で未知数 xおよびyを、4~5行目で方程式を、それぞれ定義しています。方程式は、「=0」になる形で定義しなければならないので、yを右辺に移した形に書き換えています。
2回連続で方程式を見てきましたが、一旦ここまでとしましょう。次回は、統計をテーマに平均、分散、標準偏差を学びながら、「データのバラつき」について考えてみます。
文/仙石 誠(日経BP)

文系出身者でも分かりやすいと評判の数学【再】入門書。単に数学理論を解説するだけでなく、Pythonコードで確かめられるところが好評です。
著者:谷尻かおり(メディックエンジニアリング)
価格:2500円+税
RELATED関連記事
JOB BOARD編集部オススメ求人特集
RANKING人気記事ランキング

年収2500万でも貧困層? 米マイクロソフトに18年勤務した日本人エンジニアが「日本は健全」と語るワケ

AIを「便利な道具」と思う限り、日本に勝機はない。AI研究者・鹿子木宏明が語る“ズレたAIファースト”の正体

「アジャイルの理屈を押し付けない」大手金融機関が10年かけて実践した“アジャイル文化”作りの裏側

落合陽一「2026年にはほとんどの知的作業がAIに置き換わる」人間に残される仕事は“とげ作り”

AWS認定資格12種類を一覧で解説! 難易度や費用、おすすめの学習方法も
タグ

















