データサイエンス、機械学習、ブロックチェーンなど、数学理論に裏打ちされた技術に注目が集まっています。それに従い、エンジニアにも数学の知識がより必要になってきているのは、良く耳にするところ。そこで、高校数学を学び直せるクイズを用意!さあ、あなたは何問解ける!?

問題4. おにぎりのバラつきを数値で示せますか?【Pythonで学び直す高校数学】
今回は、統計を取り上げます。統計や集合、確率は関係が深く、大量のデータに隠された傾向を分析する時などに必須の分野。AI(人工知能)や機械学習、ビッグデータやデータサイエンスなどの領域で使われます。これからのことを考えるとプログラマーとしては、しっかり押さえておきたい分野の一つです。
統計には色々な用語があり、それぞれがデータの集団の特徴を表す指標になっています。誰もが知っているのが「平均」でしょう。もし、大量のデータが2つあって、どちらの平均値も同じ値だったら、似たようなデータであると言ってしまっていいでしょうか。実は、平均値だけではデータの傾向が同じとは言い切れません。データのばらつきが違う可能性があるのです。ここでは手作りおにぎりの店を例に、データのばらつきについて見ていきましょう。
本連載ではPythonを実行する環境として、Anacondaディストリビューションのインストールを前提にしています。簡単な使い方は第1回「10進数と2進数――その違い、わかりますか?」と第2回「方程式を元にPythonでグラフを描けますか?」で解説していますが、詳しく解説しているサイトもたくさんあります。PythonやAnacondaを操作したことがないという人は、そうしたサイトもぜひ参考にしてみてください
【問題】おにぎりの重さの「そろい方」を数値で示してください
あなたはおにぎり屋さんの店長です。アルバイトに太郎くんを雇っているのですが、どうも太郎くんの握ったおにぎりは大きさが不ぞろいな気がしてなりません。そこで、自分が作ったおにぎりと太郎くんが握ったおにぎりの重さを測ってみることにしました。1週間データを集めて計算してみたところ、どちらのおにぎりも平均値は100グラムでした……。
ここで「太郎くんのおにぎりが不ぞろいなのは気のせいか」と安心してはいけません。統計データを見るときには、データ集団の形が重要です。集めたおにぎりデータの分布をグラフにしてみたところ、下の図のようになりました。
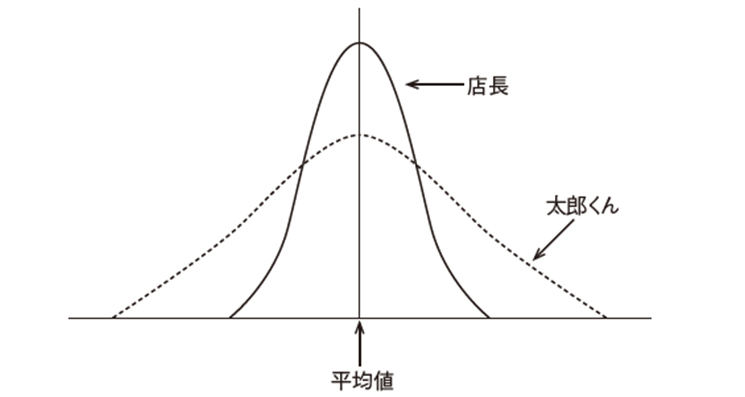
店長と太郎くんのおにぎりの度数分布図
こういったグラフを度数分布図といいます。どちらのグラフも平均値は同じです。ちなみに、このように平均値のデータ数(度数)が最も多く、左右対称の形をしている分布を正規分布といいます。2人のおにぎりデータは正規分布しているという前提で話を進めます。
この度数分布図を見ると、どちらも正規分布しており、なおかつ平均値が同じです。でも、この分布を見て、データの傾向が同じとは思えませんよね。明らかに太郎くんのおにぎりのほうがばらつきが大きいように見えます。
こういったばらつきを数値で表す指標が「分散」と「標準偏差」です。たとえば、店長と太郎くんのおにぎりの重さが、
店長…… 94 105 107 106 88
太郎…… 117 84 95 72 132
だったとしましょう。これをグラフにすると、こんな形になります。
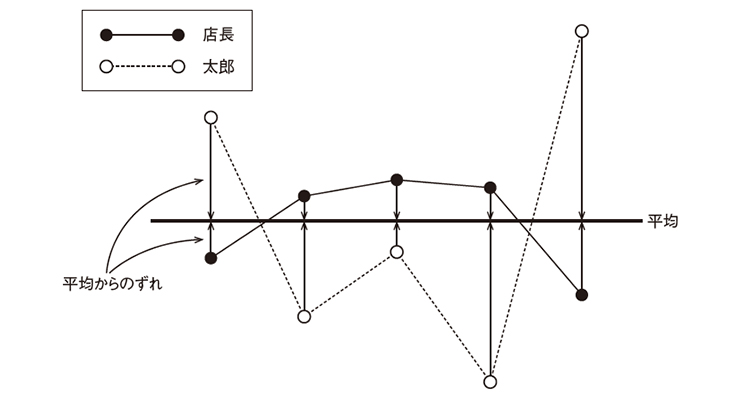
平均からのずれ
点線で表した太郎くんのほうが、平均からの「ずれ」が大きいですね。この「ずれ」を合計すれば、ばらつき具合がわかるような気がしませんか? やってみてください。
残念ながら、実際に計算してみると答えは必ずゼロになってしまいます。短いコードなので、Pythonインタプリタで確かめてみましょう。
※Pythonインタプリタの使い方は第2回「方程式をもとにPythonでグラフを描いてみましょう」を参照してください。
>>> import numpy as numpy
>>> owner = [94, 105, 107, 106, 88]
>>> mean = np.mean(owner)
>>> sum = 0
>>> for d in owner:
... sum = sum + (d - mean)
...
>>>sum
0.0
上の計算は、店長のおにぎりデータをもとに計算したものです。2行目がおにぎりのデータです。3行目でPythonのmean()関数を使って平均を求めています。次の行で、今回求めたいずれの総量となる変数sumを定義して初期化しています。
5~6行目で、おにぎりデータの個々の値でそれぞれ「値-平均」を計算し、合計しています。最後にsumでその数値を表示させていますが、何と0.0。
でも、この結果は当然なのです。すべてのデータを平らにならした値が平均値ですから、そこからの差分を合計したら答えがゼロになるのはもっともなことです。2行目を太郎くんのデータに変えて実行しても同じこと。合計は同じく0.0と変わりはありません。
※ぜひ計算してみてください。
平均を10グラム上回っているものも、10グラム下回っているものも、平均との違いという点では同じ違いとして扱いたい――。それなら値を2乗してみましょう。そうすれば符号がすべてプラスになり、合計することに意味がありそうです。上の処理を実行したPythonインタプリタに、続けて以下のコードを入力したらどうなりますか?
>>> sum = 0
>>> for d in owner:
... sum = sum + (d - mean)**2
...
>>>sum
290.0
このコードの3行目で、「個々の値-平均」の2乗を合計しています。こうすれば、ゼロではなく平均からどれだけ離れているかを数値化できそうですね。
でも、ここで求めたsumはデータ数が増えていくほど大きくなります。データ数に影響を受けないようにしないと、比較ができませんね。そこで、この値をデータ数で割ってみましょう。これが「分散」です。
ところが分散を平均とのずれとするには、数値が大きくなりすぎます。符号の影響を受けないように2乗しているためです。そこで、元に戻す計算として平方根を取ってみましょう。これが「標準偏差」です。では、Pythonインタプリタに続けて以下のコードを入力してください。
>>> import math
>>> variance = sum / 5
>>> stdev = math.sqrt(variance)
>>> variance, stdev
(58.0, 7.615773105863909)
平方根を取るのにmathライブラリのsqrt()関数を使います。このため、1行目でmathライブラリをインポートしています。2行目で分散を表す変数varianceを定義しています。3行目で標準偏差を表す変数stdevを定義しています。
分散と標準偏差は、どちらもデータのばらつき具合を示す値です。両方とも値が大きいほど、集団のデータがばらついているということを表しています。特に標準偏差は、平均からの「ぶれ」と考えるとわかりやすいかもしれません。それぞれの計算方法を確認しておきましょう。

分散と標準偏差
参考までに、前述のおにぎり5個分のデータで分散と標準偏差を求めたところ、次のような結果になりました。
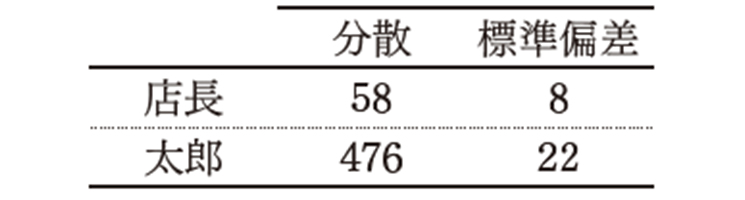
店長と太郎くんのぶれを比較
このデータがあれば、自信を持って太郎くんに注意できますね。これだけ明確な違いを見せつけられては、太郎くんは何も言えないはずです。
標準偏差と平均から偏差値を算出
「偏差値」は皆さんにもおなじみだと思います。偏差値は、データの中のある1つの値が、データ全体の中でどの位置にいるのかを示す指標です。偏差値は、全体が正規分布していることを前提としています。でも、先ほどの店長と太郎くんのおにぎりの度数分布を見てもわかる通り、正規分布といっても分布の形が違いました。この例ではたまたま平均が同じでしたが、データ集団が異なれば、平均値も違うことがほとんどでしょう。偏差値というと受験のときの模試を思い出す人も多いと思います。第1回模試と第2回模試で、平均も分布も同じということはまずないでしょう。でも比較するためには、その違いをなくさなければなりません。
こういうとき統計の世界では「標準化」という作業を行います(正規化、基準化ということもあります)。標準化は平均値が0、分散が1になるようにデータを変換する作業で、そのための式が
標準化後のデータ=(個々のデータ-平均)/標準偏差
です。標準化したデータで度数分布図を描くと、必ず下の図のような正規分布になります。
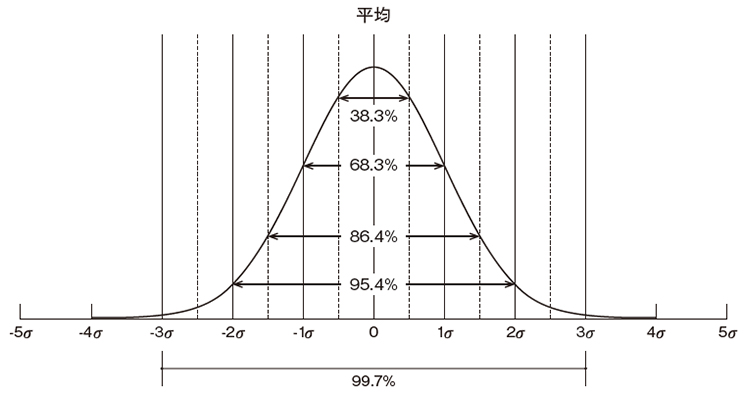
標準化された正規分布
中心から離れた値が出る確率も、図中に示したように決まります。横軸の1σ(シグマ)は標準偏差1つ分という意味です。つまり平均から±標準偏差1つ分の範囲に全体の68.3%が、±標準偏差2つ分の範囲に全体の95.4%が含まれるということです。これなら山の中心からどれだけ離れているかを見れば、それがどういう値か判断できますね。
しかし、模試の平均値が0点というのはピンと来ない値です。また、標準化したあとのデータは0.18とか-1.45といった小さな値になり、これを模試の成績と受け止めるのも難しい話です。そこでひと工夫したのが偏差値です。
偏差値では平均を50とします。それから標準化後のデータを10倍したものを加えます。式にすると以下の通りです。
標準化後のデータ=(得点-平均)/標準偏差
偏差値=標準化後のデータ×10+50
こう計算すると、模試を受けた人数や顔ぶれ、問題の難易度にかかわらず、平均点を取った人の偏差値は必ず50になります。標準化した得点を10倍して50を足しただけなので、度数分布図の形も、中心から離れた値が出る確率も同じです。つまり、自分の偏差値が山の中心(値にすると50)からどれだけ離れているかを見ることで、そのときの成績を判断できるということです。
文/仙石 誠(日経BP)

文系出身者でも分かりやすいと評判の数学【再】入門書。単に数学理論を解説するだけでなく、Pythonコードで確かめられるところが好評です。
著者:谷尻かおり(メディックエンジニアリング)
価格:2500円+税
RELATED関連記事
JOB BOARD編集部オススメ求人特集
RANKING人気記事ランキング

年収2500万でも貧困層? 米マイクロソフトに18年勤務した日本人エンジニアが「日本は健全」と語るワケ

AIを「便利な道具」と思う限り、日本に勝機はない。AI研究者・鹿子木宏明が語る“ズレたAIファースト”の正体

「アジャイルの理屈を押し付けない」大手金融機関が10年かけて実践した“アジャイル文化”作りの裏側

落合陽一「2026年にはほとんどの知的作業がAIに置き換わる」人間に残される仕事は“とげ作り”

AWS認定資格12種類を一覧で解説! 難易度や費用、おすすめの学習方法も
タグ
















