データサイエンス、機械学習、ブロックチェーンなど、数学理論に裏打ちされた技術に注目が集まっています。それに従い、エンジニアにも数学の知識がより必要になってきているのは、良く耳にするところ。そこで、高校数学を学び直せるクイズを用意!さあ、あなたは何問解ける!?

問題6.コンピューターに計算間違いさせてみよう!?【Pythonで学び直す高校数学】
「コンピューターは計算を間違えたりしない!」――。そう思っている人は多いでしょう。でも、コンピューターも間違えることはあります。間違う理由もわかるのですが、理屈はあとでOK。まずは、コンピューターに計算間違いをさせてみましょう。
まずは皆さんに計算をしていただきましょう。0.1に0.1を加えて、その答えにさらに0.1を加えて…と繰り返して、0.1を10回足し合わせてください。答えはいくつになりますか?
そう、1ですね。その計算をプログラムにしたのが、以下のコードです。これをJupyter Notebookで実行してみましょう。
本連載ではPythonを実行する環境として、Anacondaディストリビューションのインストールを前提にしています。簡単な使い方は第1回「10進数と2進数――その違い、わかりますか?」と第2回「方程式を元にPythonでグラフを描けますか?」で解説していますが、詳しく解説しているサイトもたくさんあります。PythonやAnacondaを操作したことがないという人は、そうしたサイトもぜひ参考にしてみてください
1:a = 0 2:for i in range(10): 3: a += 0.1 4:print(a)
このプログラムでは、1行目で計算結果を記録する変数aを定義して初期化します。2~3行目でaに0.1を加える処理を10回繰り返します。最後に、aの値を表示します。
これを実行した結果を見てみると…。
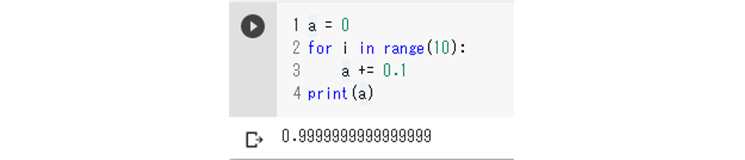
計算結果が1にならない……
何と計算が合いません。こんなに簡単な計算なのに、コンピューターが間違うなんて…。Anacondaプロンプトで0.1+0.1から順に計算してみると、0.3のところでおかしな計算結果が出てきます。でも0.4から0.7は正しく計算できる一方、0.8でまた変な数値に…。0.9以降は、0.8の変な数値に0.1が加えられている、という状況になり、1.0のところでは、上記のプログラムと同じ結果になることが確かめられるはずです。ぜひ試してみてください。
※本記事はWindows環境で検証しています。
2進数は小数に弱い
おかしな計算結果が出てきてしまうのは、コンピューターが直接取り扱う数は「0」と「1」の2種類だけということに原因があります。
私たちは通常、0から9までの数字を扱って数を数えます。この数え方のルールを「10進位取り記数法」といいます。10進法ということもあります。このルールで表した数を10進数と言います。10進位取り記数法のルールは、
・0、1、2、3、4、5、6、7、8、9の10種類の数字を使う
・並べた数字の桁は、右から順に1の位、10の位、100の位…を表す
というものです。1の位というのは100の位、10の位は101の位、100の位は102の位と見ることができます。10進位取り記数法の「10」のことを基数または底(てい)と呼びます。
コンピューターが扱う数は、基数が2、つまり2進位取り記数法(2進法)のルールに従っています。10進位取り記数法のルールに合わせて決まりを表すと、
・0、1の2種類の数字を使う
・並べた数字の桁は右から順に、20、21、22、23…を表す
となります。このルールで表した数を2進数というわけです。
では、10進数を2進数に変換してみましょう。例として、10進数の26を2進数にしてみます。それにはまず、26を2で割ります。変換後の基数で割るわけです。計算結果では、余りに注目してください。26÷2の余りは0です。この0が20の位の値になります。
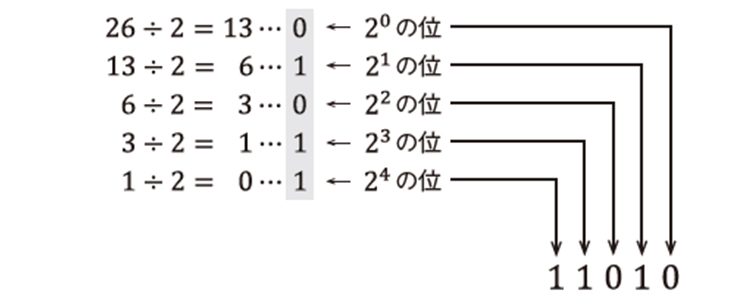
10進数の26を2進数に直す
商は次の桁の計算に使います。26÷2の商である13を2で割って、余りを21の位に…という計算を、商が0になるまで繰り返します。この結果、10進数の26は2進数で11010になります。
続いて、小数を2進数にしてみましょう。小数については、“2で割る”のではなく“2を掛ける”計算をします。例として、0.625を2進数に変換します。まず最初に0.625×2と計算します。結果である1.25の整数部分の1が2-1の桁の値になります。次に、1.25の小数部分0.25を2倍し、その結果の整数部を2-2の桁の値に…と順々に計算します。小数部が0になったらおしまいです。。

10進数の0.625を2進数に直す
元の10進数が「26.625」だったら、整数部分と小数部分をそれぞれこのように計算して「11010.101」と変換すればいいのです。ところが0.1は、そううまくは行きません。
実は0.1は2進数ではぴったりには書き表せない数なのです。上記の計算に従って2進数に直してみると、いつまで2倍しても小数部が0になりません。2進数の各桁の値を求めると「0.000110011001100…」となり、以降1100を繰り返します。整数であれば問題ないのですが、実数となると正しく2進数に変換できない数が出てきます。
※今回は取り上げませんが、整数であっても扱える数には範囲に限りがあります。
コンピューターは無限に桁が続く数字は扱えません。扱える桁には上限があります。どこかで打ち切って残りを切り捨てないとなりません。これが誤差になります。冒頭で紹介した0.1のたし算プログラムは、0.1を10回足し合わせているようで実は0.1とはちょっと違う数のたし算をしているというわけです。
原因がわかっていれば計算間違い対策は可能
0.1のたし算であれば、その誤差が影響しないこともあります。冒頭のプログラムで10回足し合わせるところを、2回もしくは4~7回で実行すると正しく計算できることがわかります。でも、だからと言って精密な結果が求められるプログラムでは目をつぶるわけにはいきません。
そこで冒頭のプログラムを、小数を小数のまま扱うのではなく、整数に変換して誤差が生じないように書き換えてみました。
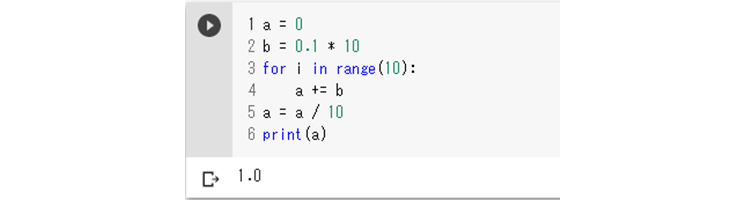
1:a = 0 2:b = 0.1 * 10 3:for i in range(10): 4: a += b 5:a = a / 10 6:print(a)
2行目に新たな変数bを追加したのが工夫です。変数bに0.1を10倍した値を定義します。実際に10回足し合わせる計算は、0.1ではなくbで実行します(4行目)。これにより、実数のたし算に伴う誤差を回避できるというわけです。
2行目で10倍したので、5行目で計算結果を1/10にしました。これで正しく計算できるプログラムになりました。
文/仙石 誠(日経BP)

文系出身者でも分かりやすいと評判の数学【再】入門書。単に数学理論を解説するだけでなく、Pythonコードで確かめられるところが好評です。
著者:谷尻かおり(メディックエンジニアリング)
価格:2500円+税
RELATED関連記事
JOB BOARD編集部オススメ求人特集
RANKING人気記事ランキング

年収2500万でも貧困層? 米マイクロソフトに18年勤務した日本人エンジニアが「日本は健全」と語るワケ

AIを「便利な道具」と思う限り、日本に勝機はない。AI研究者・鹿子木宏明が語る“ズレたAIファースト”の正体

「アジャイルの理屈を押し付けない」大手金融機関が10年かけて実践した“アジャイル文化”作りの裏側

落合陽一「2026年にはほとんどの知的作業がAIに置き換わる」人間に残される仕事は“とげ作り”

AWS認定資格12種類を一覧で解説! 難易度や費用、おすすめの学習方法も
タグ

















